اخترعت عائلة سمبسون هذه المهمة الهندسية الصعبة بشكل مدهش

مختبئًا وسط هجاء علامته التجارية للحياة الأمريكية المتوسطة، عائلة سمبسون مليء ببيض عيد الفصح الرياضي. يتباهى طاقم كتابة العرض بنسب مثيرة للإعجاب من خبراء الرياضيات في Ivy League الذين لم يتمكنوا من مقاومة غرس أطول المسرحية الهزلية في أمريكا مع النكات الداخلية، المنتشرة مثل الرش على كعك هوميروس.

في وقت مبكر من اللقطة الافتتاحية للحلقة الثانية من العرض، تقوم الطفلة ماجي البالغة من العمر عامًا واحدًا بتكديس مكعبات الأبجدية الخاصة بها لقراءة EMCSQU. لا شك أنه تكريم لمعادلة أينشتاين الشهيرة ه = مولودية².

هناك حلقة يحاول فيها هومر أن يصبح مخترعًا ويصمم بعض الأفكار الطائشة، بما في ذلك بندقية تزيل المكياج على وجهك وكرسي مزود بمرحاض مدمج. أثناء جنون العصف الذهني، كتب هوميروس بعض المعادلات على السبورة بما في ذلك:

1987¹² + 4365¹² = 4472¹²

يشير هذا إلى نظرية فيرما الأخيرة، وهي واحدة من أكثر المعادلات شهرة في تاريخ الرياضيات. النسخة المحفوظة بوعاء، إذا لم تكن قد صادفتها: كتب عالم الرياضيات بيير دي فيرما في القرن السابع عشر أن المعادلة أ^ن + ب^ن = ج^ن ليس لديه حلول أعداد صحيحة عندما يكون n أكبر من 2. بمعنى آخر، لا يمكنك العثور على ثلاثة أرقام صحيحة (أرقام غير عشرية مثل 1، 2، 3…) أ, ب، و ج مثل ذلك أ³ + ب³ = ج³ أو أ⁴ + ب⁴ = ج⁴، وما إلى ذلك وهلم جرا. كتب فيرما أنه “اكتشف دليلاً رائعًا حقًا على ذلك” لكنه لم يستطع وضعه في هامش نصه. وجد علماء الرياضيات في وقت لاحق هذه الرسالة، وعلى الرغم من المظهر البسيط للادعاء، فشلوا في إثبات ذلك. لقد ظل دون إثبات لأكثر من أربعة قرون حتى حله أندرو وايلز أخيرًا في عام 1994. ويعتمد إثبات ويلز على تقنيات أكثر تقدمًا بكثير مما كان متاحًا في أيام فيرما، مما يترك الباب مفتوحًا أمام احتمال محير بأن فيرما كان على علم بدليل أكثر أولية على أننا لدينا. لم يتم اكتشافه بعد (أو أن دليله المفترض به خطأ).

أدخل معادلة هوميروس في الآلة الحاسبة الخاصة بك. إنه يتحقق! فعل عائلة سمبسون العثور على مثال مضاد لنظرية فيرما الأخيرة؟ اتضح أن أرقام هوميروس الثلاثية تشكل خطأً وشيكًا. لا تعرض معظم الآلات الحاسبة الدقة الكافية لاكتشاف التناقض الطفيف بين طرفي المعادلة. كتب الكاتب ديفيد إكس كوهين برنامجه الحاسوبي الخاص للبحث عن حلول شبه مستحيلة لمعادلة فيرما سيئة السمعة، كل هذا من أجل هذه الكمامة التي لا تكاد تذكر.

يأتي لغز هذا الأسبوع من خاتمة الموسم 26، حيث يشارك سكان سبرينجفيلد في مسابقة للرياضيين. الحلقة مليئة بالأشياء الرياضية الجيدة، بما في ذلك النكتة الصغيرة أدناه المنشورة خارج المنافسة. هل يمكنك فك تشفيرها؟

إن مشكلة هندسة كسر التعادل المناخية أصعب مما تبدو. آمل ألا يجعلك تصرخ “D’oh!”

هل فاتتك لغز الأسبوع الماضي؟ تحقق من ذلك هنا، وتجد حلها في أسفل مقال اليوم. احرص على عدم القراءة كثيرًا إذا لم تكن قد قمت بحل مشكلة الأسبوع الماضي بعد!

اللغز رقم 20: عائلة سمبسون م

أضف ثلاثة خطوط مستقيمة إلى الرسم التخطيطي لإنشاء تسعة مثلثات غير متداخلة.

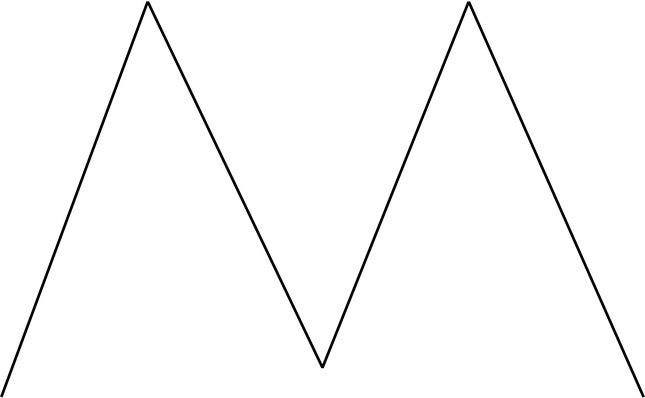
قد تتشارك المثلثات في الجوانب، لكن لا ينبغي أن تتشارك في المساحة الداخلية. على سبيل المثال، الشكل الأيسر أدناه يصور مثلثين، في حين أن الشكل الأيمن يعتبر مثلثًا واحدًا فقط، لأن المثلث الأكبر يتداخل مع المثلث الأصغر.

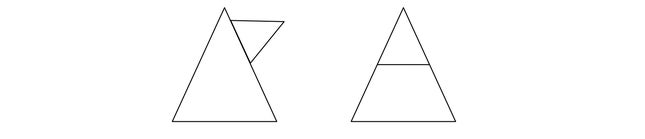
سأنشر الإجابة يوم الاثنين القادم مع لغز جديد. هل تعرف لغزًا رائعًا تعتقد أنه يجب عرضه هنا؟ راسلني على تويتر @ جاكبمورتاغ أو راسلني عبر البريد الإلكتروني على gizmodopuzzle@gmail.com

حل اللغز رقم 19: الأوهام العقلية

كيف كان أدائك في الأسبوع الماضي مشاكل؟ لقد قارنتها بالأوهام البصرية لأن كلا اللغزين يبدوان للوهلة الأولى وكأنهما يتطلبان بعض العمليات الحسابية. ولكن بمجرد أن تدرك الخدعة الخفية، فإن الحل يستقر في التركيز مكعبات نيكر انقلاب فجأة. كلا اللغزين هما في الواقع لعبة gimmes، بالمنظور الصحيح. تحية للقارئ ماكاي، الذي أرسل إجابتين صحيحتين عبر البريد الإلكتروني.

1. سوف يستغرق الأمر دقيقة واحدة على الأكثر حتى يسقط جميع النمل من نهاية العصا المترية. يبدو الأمر معقدًا لتتبع السلوك المتذبذب لكل نملة. ألا يمكنهم التأرجح ذهابًا وإيابًا إلى الأبد؟ عندما تغمض عينيك، سترى أن الحالة التي يقوم فيها نملتان متصادمتان بتبديل اتجاهاتهما على الفور لا تختلف عن الحالة التي يتحرك فيها النمل مباشرة عبر بعضهما البعض! في كلتا الحالتين، سيكون هناك نمل في نفس النقاط تمامًا على طول العصا ويسير في نفس الاتجاه.

تخيل أن كل نملة كانت ترتدي قبعة صغيرة، وعندما تصطدم نملتان، تقومان بتبادل القبعات على الفور قبل الاستمرار في الاتجاه المعاكس. تتبع مسار قبعة واحدة وستلاحظ أنها مجرد خطوط مباشرة لطرف واحد من العصا بوتيرة ثابتة طوال الوقت. نظرًا لأن النمل يتحرك بسرعة متر واحد في الدقيقة، وأطول مسافة يمكن أن تقطعها أي نملة هي الطول الكامل للعصا المترية، فإن جميع النمل سيصل إلى نهاية العصا خلال دقيقة واحدة.

2. ماذا عن مشكلة الهندسة؟

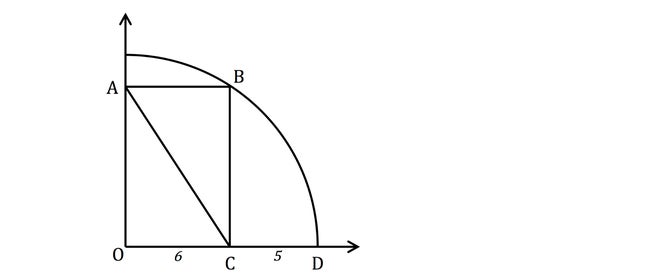
ما هو طول التيار المتردد؟

يبدو جاهزًا لـ SAT. ربما نظرية فيثاغورس في محلها. ربما هوية مثلثية أو اثنتين. ومض مرتين وسيختفي وهم التعقيد. الخط الذي يربط النقطتين O و B هو أيضًا قطري للمستطيل وسيكون له نفس طول AC. فقط OB هو الأكثر فائدة لأنه نصف قطر الدائرة! يخبرنا الرسم البياني بنصف قطر الدائرة على طول المحور السيني: 6+5 = 11، إجابتنا.